SVD Image Compression
Shows an k-rank matrix of an image computed with an svd.
Short Explanation
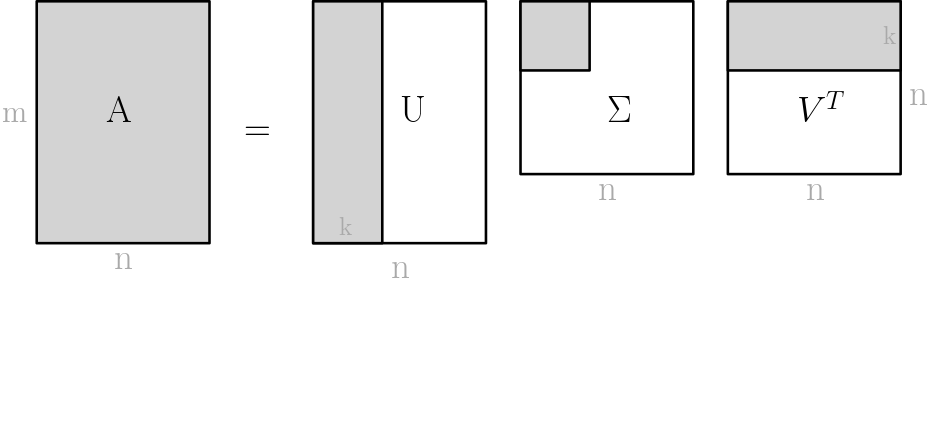
An image can be represented with a matrix with each pixel value corresponding to an entry. We can then compute a singular value decomposition (svd) of this matrix A = UΣVT.If we only keep the first k columns of U and the first k columns of VT, we approximate the matrix A (displayed in gray below).
Since the values in Σ are sorted by size, we only discard the rows with a small value, thus not loosing too much information. This can be seen in the image above. If we discard half the entries the image is still recognisable. (Note: the effectiveness depends on the image)